Heap - 堆

1. Heap - 堆

• 堆分为两种：最大堆和最小堆，两者的差别在于节点的排序方式

• 堆是一棵完全树（complete tree）：即除了最底层，其他层的节点都被元素填满，且最底层尽可能地从左到右填入

• 在最大堆中，父节点的值比每一个子节点的值都要大。在最小堆中，父节点的值比每一个子节点的值都要小。这就是所谓的“堆属性”，并且这个属性对堆中的每一个节点都成立

  

• 而对于最小堆，根节点中的元素总是树中的最小值。堆属性非常有用，因为堆常常被当做优先队列使用，因为可以快速地访问到“最重要”的元素

  

  

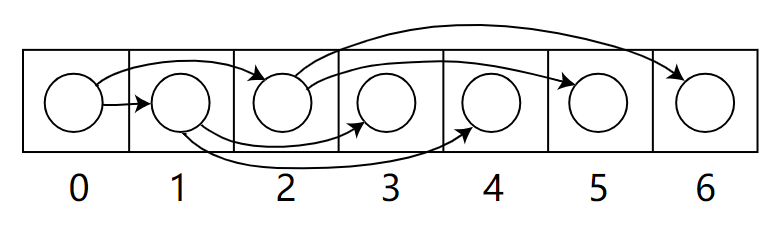
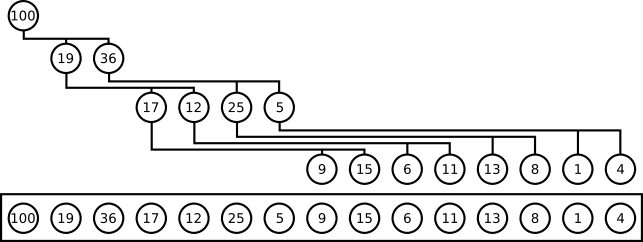
• **注意：**堆的根节点中存放的是最大或者最小元素，但是其他节点的排序顺序是未知的。例如，在一个最大堆中，最大的那一个元素总是位于 index 0 的位置，但是最小的元素则未必是最后一个元素。--唯一能够保证的是最小的元素是一个叶节点，但是不确定是哪一个

2. 堆与搜索二叉树的区别

• 堆并不能取代二叉搜索树，它们之间有相似之处也有一些不同。我们来看一下两者的主要差别：
  1. **节点的顺序：**在二叉搜索树中，左子节点必须比父节点小，右子节点必须必比父节点大。但是在堆中并非如此。在最大堆中两个子节点都必须比父节点小，而在最小堆中，它们都必须比父节点大。
  2. **内存占用：**普通树占用的内存空间比它们存储的数据要多。你必须为节点对象以及左/右子节点指针分配内存。堆仅仅使用一个数据来存储数组，且不使用指针。
  3. 平衡：二叉搜索树必须是“平衡”的情况下，其大部分操作的复杂度才能达到O(log n)。你可以按任意顺序位置插入/删除数据，或者使用 AVL 树或者红黑树，但是在堆中实际上不需要整棵树都是有序的。我们只需要满足堆属性即可，所以在堆中平衡不是问题。因为堆中数据的组织方式可以保证O(log n) 的性能
  4. **搜索:**在二叉树中搜索会很快，但是在堆中搜索会很慢。在堆中搜索不是第一优先级，因为使用堆的目的是将最大（或者最小）的节点放在最前面，从而快速的进行相关插入、删除操作

3. container/heap

• 实现接口一共有五个（sort.Interface 3个 + heap.Interface 2个）

  // sort.Interface
  type Interface interface {
  	// Len is the number of elements in the collection.
  	Len() int
  	// Less reports whether the element with index i must sort before the element with index j.
  	Less(i, j int) bool
  	// Swap swaps the elements with indexes i and j.
  	Swap(i, j int)
  }
  
  // heap.Interface
  type Interface interface {
  	sort.Interface
  	Push(x any) // add x as element Len()
  	Pop() any   // remove and return element Len() - 1.
  }
  

• 其中heap包单独暴露了一些方法：

  • 接口都需要传入上述接口的实例化对象

  • 不要混淆heap.Push和自己slice实现的Push方法

    • 开发者实现的Push方法仅仅是对slice操作 heap.Push调用了slice的Push操作，还需要额外的调整用以维护heap性质

  // 建堆， 对heap进行初始化，生成小根堆（或大根堆）
  func Init(h Interface)
  // 插入元素
  func Push(h Interface, x interface{})
  // 弹出root元素
  func Pop(h Interface) interface{}
  // Update元素(包括优先级)，从i位置数据发生改变后，对堆再平衡，优先级队列的实现会使用此方法
  func Fix(h Interface, i int)
  // 删除，从指定位置删除数据，并返回删除的数据，同时亦涉及到堆的再平衡
  func Remove(h Interface, i int) interface{}
  

3.1 Init

• Init 为初始化建立 heap 的方法, 该方法调用了heap.down 方法

• 在 Init 方法中，调整的位置，第 1 个的元素的位置是 n/2-1 个，符合最小堆的特性；最后一个位置是堆顶的位置 0

• heap.down 方法的作用是，任选一个元素 i，将与其子节点 2i+1 和 2i+2 比较，如果 i 比它的子节点小，则将 i 与两个子节点中较小的节点交换（代码中的 j）；子节点 j 再与它的子节点，继续比较、交换，直到数组末尾、或者待比较的元素比它的两个子节点都小，跳出当前的 heap.down 循环

  // A heap must be initialized before any of the heap operations
  // can be used. Init is idempotent with respect to the heap invariants
  // and may be called whenever the heap invariants may have been invalidated.
  // Its complexity is O(n) where n = h.Len().
  //
  func Init(h Interface) {
  	// heapify
  	n := h.Len()	//堆长度，下标从0 ~ n-1
  	for i := n/2 - 1; i >= 0; i-- {
  		// 从长度的一半开始，一直到第0个数据，每个位置都调用down方法，down方法实现的功能是保证从该位置往下保证形成堆
  		down(h, i, n)
  	}
  }
  
  // 给定类型，需要调整的元素在数组中的索引以及 heap 的长度
  // 将该元素下沉到该元素对应的子树合适的位置，从而满足该子树为最小堆
  func down(h Interface, i0, n int) bool {
  	i := i0	// 中间变量，初始化保存为：往下调整为heap所在的节点位置
  	for {
  		j1 := 2*i + 1	// i节点的左子孩子
  		if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
  			// 如果j1 越界了，说明已经调整完成了，可以退出循环
  			break
  		}
  		j := j1 // left child
  
  		//中间变量j先赋值为左子孩子，之后j将被赋值为左右子孩子中最小（大）的一个孩子的位置
  		if j2 := j1 + 1; j2 <n && h.Less(j2, j1) {
  			j = j2 // = 2*i + 2 // right child
  		}
  		//j被赋值为两个孩子中的最小（大）孩子的位置（由开发者实现的Less方法决定）
  		if !h.Less(j, i) {
        		// 比较孩子和当前的父亲节点，如果满足堆的要求了，退出循环（注意：j在前，i在后，结果取非）
  			break
  		}
  		h.Swap(i, j) // 否则交换i和j位置的值，继续比较
  		i = j		// 保存j的位置，继续向下调整，保证j位置的子树是heap结构
  	}
  
  	//这个结果有点意思：如果i>i0，说明调整了，返回true；否则，未调整返回false
  	return i > i0
  }
  

  

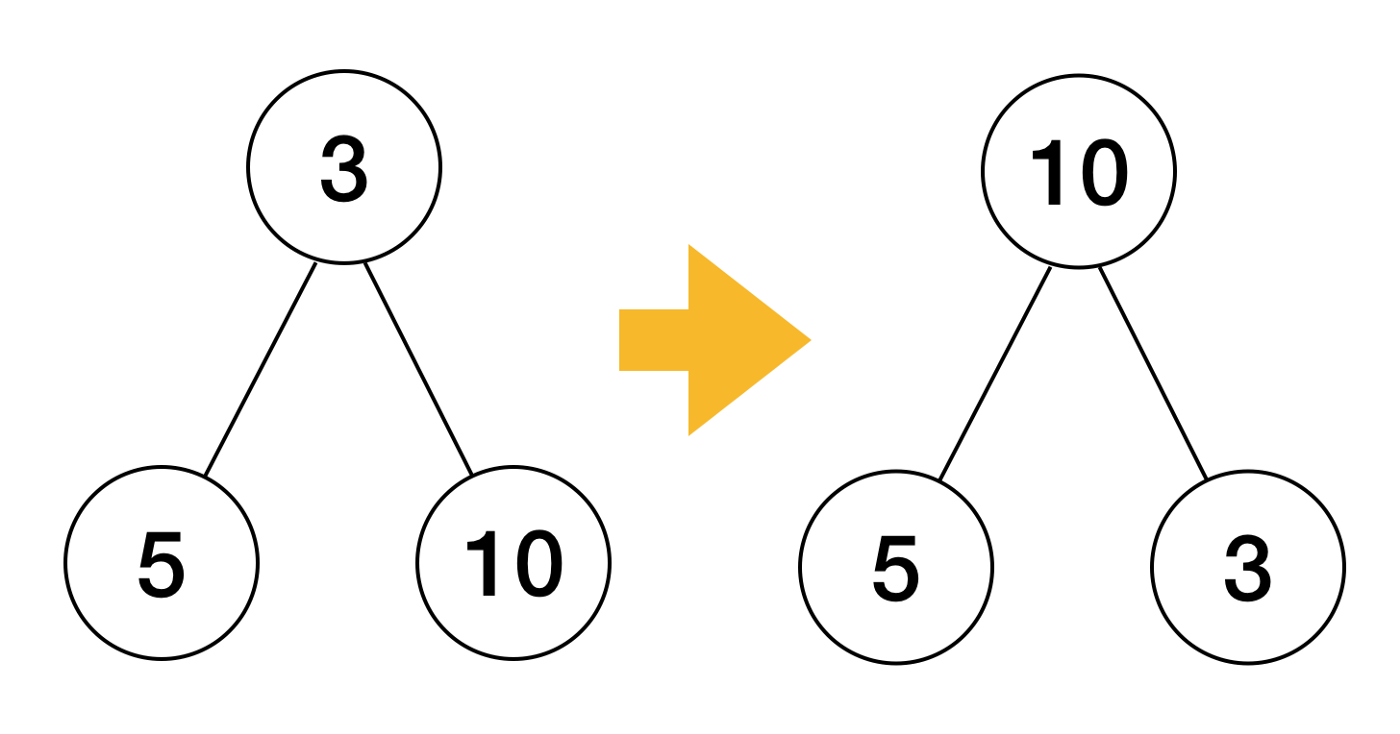
3.2 Push

• Push 方法保证插入新元素时，顺序数组 h 仍然是一个 heap；和上面的描述一致，将 x 元素插入到了数组的末尾位置，再调用 up 方法自下而上进行调整，使其满足 heap 的性质

• heap.up 方法也较易理解：依此（for loop）查找元素 j 的父节点（i），如果 j 比父节点 i 要小，则交换这两个节点，并继续向再上一级的父节点比较，直到根节点，或者元素 j 大于 父节点 i（调整完毕，无需再继续进行）

  // Push pushes the element x onto the heap. The complexity is
  // O(log(n)) where n = h.Len().
  func Push(h Interface, x interface{}) {
  	// 将新插入进来的节点放到最后（调用开发者封装的Push）
  	h.Push(x)
  	// 自下而上调整
  	up(h, h.Len()-1)
  }
  
  func up(h Interface, j int) {
  	for {
  		i := (j - 1) / 2 // parent（j节点的父节点）
  		if i == j || !h.Less(j, i) {
  			// 如果越界，或者满足堆的条件（使用开发者实现的Less方法），则结束for循环
  			break
  		}
  		// 否则将该节点和父节点交换，继续下一轮比较
  		h.Swap(i, j)
  		j = i	// 交换当前位置，对父节点继续进行检查直到根节点
  	}
  }
  

3.3 Pop

• heap.Pop 方法是取出堆顶位置的数据（minheap 为最小），取完数据之后，heap 肯定不平衡。所以通常的做法是：将根节点（0 位置）与末尾节点的元素交换，并将新的根节点的元素（先前的最后一个元素）down 自上而下调整到合适的位置，满足最小堆的要求

• 最后再调用用户自定义的 Pop 函数获取最后一个元素即可; 这里需要区分 heap 包的 Pop 方法和用户自定义实现的 Pop 方法的根本区别，用户的 Pop 方法只是用来获取数据的

  // Pop removes the minimum element (according to Less) from the heap
  // and returns it. The complexity is O(log(n)) where n = h.Len().
  // It is equivalent to Remove(h, 0).
  func Pop(h Interface) interface{} {
  	// 把最后一个节点和第一个节点进行交换，之后，从根节点开始重新保证堆结构，最后把最后那个节点数据丢出并返回
  	n := h.Len() - 1
  	h.Swap(0, n)
  	down(h, 0, n)
  	return h.Pop()
  }
  

3.4 Remove

• Remove 方法提供了删除指定位置 index 元素的实现，即先将要删除的节点 i 与末尾节点 n 交换，然后将新的节点 i 下沉或上浮到合适的位置（通俗的说，由于新数据调整，原先末尾的位置升到了它不该在的位置，需要调整这个元素，先一路 down 到底，然后再一路 up 到最终的位置）

  // Remove removes the element at index i from the heap.
  // The complexity is O(log(n)) where n = h.Len().
  //
  func Remove(h Interface, i int) interface{} {
  	n := h.Len() - 1
  	if n != i {
  		//Pop只是Remove的特例
  		//Remove是把i位置的节点和最后一个节点进行交换，之后保证从i节点往下及往上都保证堆结构，最后把最后一个节点的数据返回
  		h.Swap(i, n)
  		if !down(h, i, n) {
  			up(h, i)
  		}
  	}
  	return h.Pop()
  }
  

3.5 Fix

• Fix 方法的意义是在优先级队列的场景（从 i 位置数据发生改变后，对 heap 再平衡，优先级队列会使用本方法）。即当i节点的比较值发生改变后，需要保证heap的再平衡：先调用down保证该节点下面的堆结构，如果有位置交换，则需要保证该节点往上的堆结构，否则就不需要往上保证堆结构（没有调整影响另一侧的话，肯定是平衡的）。

  // Fix re-establishes the heap ordering after the element at index i has changed its value.
  // Changing the value of the element at index i and then calling Fix is equivalent to,
  // but less expensive than, calling Remove(h, i) followed by a Push of the new value.
  // The complexity is O(log(n)) where n = h.Len().
  func Fix(h Interface, i int) {
  	if !down(h, i, h.Len()) {
  		up(h, i)
  	}
  }
  

4. 应用场景

• 定时器
• 优先级队列：比如kubernetes中的实现，FIFO-PriorityQueue (opens new window)
• heap排序

5. 代码示例

5.1 IntHeap

• code

  // This example demonstrates an integer heap built using the heap interface.
  package heap_test
  
  import (
  	"container/heap"
  	"fmt"
  )
  
  // An IntHeap is a min-heap of ints.
  type IntHeap []int
  
  func (h IntHeap) Len() int           { return len(h) }
  func (h IntHeap) Less(i, j int) bool { return h[i] < h[j] }
  func (h IntHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }
  
  func (h *IntHeap) Push(x any) {
  	// Push and Pop use pointer receivers because they modify the slice's length,
  	// not just its contents.
  	*h = append(*h, x.(int))
  }
  
  func (h *IntHeap) Pop() any {
  	old := *h
  	n := len(old)
  	x := old[n-1]
  	*h = old[0 : n-1]
  	return x
  }
  
  // This example inserts several ints into an IntHeap, checks the minimum,
  // and removes them in order of priority.
  func Example_intHeap() {
  	h := &IntHeap{2, 1, 5}
  	heap.Init(h)
  	heap.Push(h, 3)
  	fmt.Printf("minimum: %d\n", (*h)[0])
  	for h.Len() > 0 {
  		fmt.Printf("%d ", heap.Pop(h))
  	}
  	// Output:
  	// minimum: 1
  	// 1 2 3 5
  }
  
  

5.2 PriorityQueue 优先队列

• code

  // This example demonstrates a priority queue built using the heap interface.
  package heap_test
  
  import (
  	"container/heap"
  	"fmt"
  )
  
  // An Item is something we manage in a priority queue.
  type Item struct {
  	value    string // The value of the item; arbitrary.
  	priority int    // The priority of the item in the queue.
  	// The index is needed by update and is maintained by the heap.Interface methods.
  	index int // The index of the item in the heap.
  }
  
  // A PriorityQueue implements heap.Interface and holds Items.
  type PriorityQueue []*Item
  
  func (pq PriorityQueue) Len() int { return len(pq) }
  
  func (pq PriorityQueue) Less(i, j int) bool {
  	// We want Pop to give us the highest, not lowest, priority so we use greater than here.
  	return pq[i].priority > pq[j].priority
  }
  
  func (pq PriorityQueue) Swap(i, j int) {
  	pq[i], pq[j] = pq[j], pq[i]
  	pq[i].index = i
  	pq[j].index = j
  }
  
  func (pq *PriorityQueue) Push(x any) {
  	n := len(*pq)
  	item := x.(*Item)
  	item.index = n
  	*pq = append(*pq, item)
  }
  
  func (pq *PriorityQueue) Pop() any {
  	old := *pq
  	n := len(old)
  	item := old[n-1]
  	old[n-1] = nil  // avoid memory leak
  	item.index = -1 // for safety
  	*pq = old[0 : n-1]
  	return item
  }
  
  // update modifies the priority and value of an Item in the queue.
  func (pq *PriorityQueue) update(item *Item, value string, priority int) {
  	item.value = value
  	item.priority = priority
  	heap.Fix(pq, item.index)
  }
  
  // This example creates a PriorityQueue with some items, adds and manipulates an item,
  // and then removes the items in priority order.
  func Example_priorityQueue() {
  	// Some items and their priorities.
  	items := map[string]int{
  		"banana": 3, "apple": 2, "pear": 4,
  	}
  
  	// Create a priority queue, put the items in it, and
  	// establish the priority queue (heap) invariants.
  	pq := make(PriorityQueue, len(items))
  	i := 0
  	for value, priority := range items {
  		pq[i] = &Item{
  			value:    value,
  			priority: priority,
  			index:    i,
  		}
  		i++
  	}
  	heap.Init(&pq)
  
  	// Insert a new item and then modify its priority.
  	item := &Item{
  		value:    "orange",
  		priority: 1,
  	}
  	heap.Push(&pq, item)
  	pq.update(item, item.value, 5)
  
  	// Take the items out; they arrive in decreasing priority order.
  	for pq.Len() > 0 {
  		item := heap.Pop(&pq).(*Item)
  		fmt.Printf("%.2d:%s ", item.priority, item.value)
  	}
  	// Output:
  	// 05:orange 04:pear 03:banana 02:apple
  }
  
  

List - 双向链表

0. 结构

type List struct {
	root Element // sentinel list element, only &root, root.prev, and root.next are used
	len  int     // current list length excluding (this) sentinel element
}

type Element struct {
	next, prev *Element
	list *List
	Value any
}

1. 代码示例

• code

  func Example() {
  	// Create a new list and put some numbers in it.
  	l := list.New()
  	e4 := l.PushBack(4)
  	e1 := l.PushFront(1)
  	l.InsertBefore(3, e4)
  	l.InsertAfter(2, e1)
  
  	// Iterate through list and print its contents.
  	for e := l.Front(); e != nil; e = e.Next() {
  		fmt.Println(e.Value)
  	}
  
  	// Output:
  	// 1
  	// 2
  	// 3
  	// 4
  }
  

2. Element的方法

func (e *Element) Next() *Element // 返回该元素的下一个元素，如果没有下一个元素则返回 nil
func (e *Element) Prev() *Element // 返回该元素的前一个元素，如果没有前一个元素则返回 nil

3. List的方法

func New() *List                                                    // 构造一个初始化的list
func (l *List) Back() *Element                                      // 获取list l的最后一个元素
func (l *List) Front() *Element                                     // 获取list l的最后一个元素
func (l *List) Init() *List                                         // list l 初始化或者清除 list l
func (l *List) InsertAfter(v interface{}, mark *Element) *Element   // 在 list l 中元素 mark 之后插入一个值为 v 的元素，并返回该元素，如果 mark 不是list中元素，则 list 不改变
func (l *List) InsertBefore(v interface{}, mark *Element) *Element  // 在 list l 中元素 mark 之前插入一个值为 v 的元素，并返回该元素，如果 mark 不是list中元素，则 list 不改变
func (l *List) Len() int                                            // 获取 list l 的长度
func (l *List) MoveAfter(e, mark *Element)                          // 将元素 e 移动到元素 mark 之后，如果元素e 或者 mark 不属于 list l，或者 e==mark，则 list l 不改变
func (l *List) MoveBefore(e, mark *Element)                         // 将元素 e 移动到元素 mark 之前，如果元素e 或者 mark 不属于 list l，或者 e==mark，则 list l 不改变
func (l *List) MoveToBack(e *Element)                               // 将元素 e 移动到 list l 的末尾，如果 e 不属于list l，则list不改变 
func (l *List) MoveToFront(e *Element)                              // 将元素 e 移动到 list l 的首部，如果 e 不属于list l，则list不改变 
func (l *List) PushBack(v interface{}) *Element                     // 在 list l 的末尾插入值为 v 的元素，并返回该元素 
func (l *List) PushBackList(other *List)                            // 在 list l 的尾部插入另外一个 list，其中l 和 other 可以相等 
func (l *List) PushFront(v interface{}) *Element                    // 在 list l 的首部插入值为 v 的元素，并返回该元素 
func (l *List) PushFrontList(other *List)                           // 在 list l 的首部插入另外一个 list，其中 l 和 other 可以相等 
func (l *List) Remove(e *Element) interface{}                       // 如果元素 e 属于list l，将其从 list 中删除，并返回元素 e 的值

4. 应用场景

• 时间轮的任务链表定义 (opens new window)
• Cache中实现LRU机制的链式结构 (opens new window)

5. 注意问题与坑

5.1 注意问题

1. 不要使用自己构造的Element结构，作为参数传入List的方法
2. Remove方法是传入指定位置的元素（list的Remove实现），复杂度是O(1)，需要开发者保存对应的element的指针（地址）
3. 若在goroutine并发环境下使用container/list链表，那么需要加锁
4. List并未提供Pop类方法，需要自行组合实现，不过需要加锁
5. List包中大部分对于e *Element进行操作的元素都可能会导致程序崩溃，其根本原因是e是一个Element类型的指针，当然其也可能为nil，但是go中list包中函数没有对其进行是否为nil的检查，变默认其非nil进行操作，所以这种情况下，便可能出现程序崩溃

5.2 坑

1. 遍历删除List中的所有元素, 遍历删除不安全

   • 问题code:注意到返回被删除的Element时，会将e.next = nil

     func main() {
     	l := list.New()
     	l.PushBack(1)
     	l.PushBack(2)
     	l.PushBack(3)
     	l.PushBack(4)
     
     	// 遍历list，删除元素
     	for e := l.Front(); e != nil; e = e.Next() {
     		fmt.Println("removing", e.Value)
     		l.Remove(e)
     	}
     	fmt.Println("After Removing...")
     	// 遍历删除完元素后的list
     	for e := l.Front(); e != nil; e = e.Next() {
     		fmt.Println(e.Value)
     	}
     }
     

2. List大部分方法不检查传入参数为nil

3. 并发不安全

Ring - 环形链表

0. 结构

type Ring struct {
    next *Ring
	prev  *Ring
    Value  interface{}
}

1. 代码示例

• code

  func main() {
  	// 创建一个环, 包含 3 个元素
  	r := ring.New(3)
  	fmt.Printf("ring: %+v\n", *r)
  
  	// 初始化
  	for i := 1; i <= 3; i++ {
  		r.Value = i
  		r = r.Next()
  	}
  	fmt.Printf("init ring: %+v\n", *r)
  
  	// sum
  	s := 0
  	r.Do(func(i interface{}) {
          fmt.Println(i)
  		s += i.(int)
  	})
  	fmt.Printf("sum ring: %d\n", s)
  }
  

2. Ring 方法

func New(n int) *Ring               // 用于创建一个新的 Ring, 接收一个整形参数，用于初始化 Ring 的长度 
func (r *Ring) Len() int            // 环长度

func (r *Ring) Next() *Ring         // 返回当前元素的下个元素
func (r *Ring) Prev() *Ring         // 返回当前元素的上个元素
func (r *Ring) Move(n int) *Ring    // 指针从当前元素开始向后移动或者向前(n 可以为负数)

// Link & Unlink 组合起来可以对多个链表进行管理
func (r *Ring) Link(s *Ring) *Ring  // 将两个 ring 连接到一起 (r 不能为空)
func (r *Ring) Unlink(n int) *Ring  // 从当前元素开始，删除 n 个元素

func (r *Ring) Do(f func(interface{}))  // Do 会依次将每个节点的 Value 当作参数调用这个函数 f, 实际上这是策略方法的引用，通过传递不同的函数以在同一个 ring 上实现多种不同的操作。

3. 应用场景

1. 构造定长环回队列，如保存固定长度的数据等
2. 用作固定长度的对象缓冲区（参见goim的数据结构分析）

4. ring 和 list的区别

• Ring 类型的数据结构仅由它自身即可代表，而 List 类型则需要由它以及 Element 类型联合表示
• 一个 Ring 类型的值严格来讲，只代表了其所属的循环链表中的一个元素，而一个 List 类型的值则代表了一个完整的链表
• 在创建并初始化一个 Ring 时，可以指定它包含的元素数量，但是对于一个 List 值来说却不需要。循环链表一旦被创建，其长度是不可变的
• 通过 var r ring.Ring 声明的 r 将会是一个长度为 1 的循环链表，而 List 类型的零值则是一个长度为 0 的链表。)（List 中的根元素不会持有实际元素的值）
• Ring 的 Len 方法的算法复杂度是 O(N)，而 List 的 Len 算法复杂度是 O(1)